Si \(\mathscr R\) est une relation d'équivalence sur \(E\), la classe d'équivalence de \(x\in E\) est définie par : $${{\operatorname{cl}(x)=\bar x}}={{\{y\in E\mid y\mathscr R x\} }}$$
(Ensemble, Relation d’équivalence)
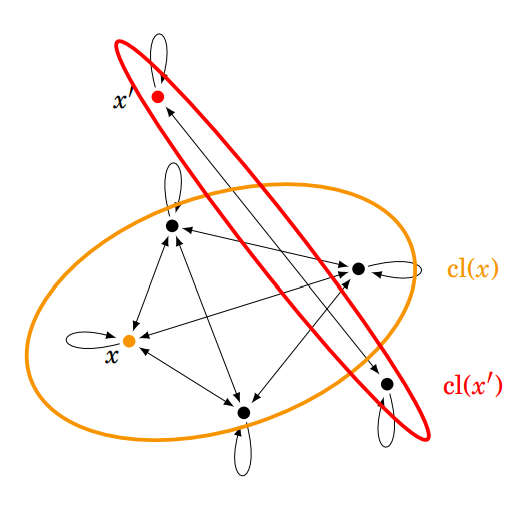
un représentant de la classe \(\operatorname{cl}(x)\) est un élément \(y\in\operatorname{cl}(x)\)
$${{\operatorname{cl}(x)=\operatorname{cl} (y)}}\iff {{x\mathscr Ry}}$$
$$\forall x,y\in E,\quad{{(\operatorname{cl}(x)=\operatorname{cl}(y))}}\lor{{(\operatorname{cl}(x)\cap\operatorname{cl}(y)=\varnothing)}}$$
(Ensembles disjoints)
Si \(C\) est un ensemble de représentants de toutes les classes, alors \(\{\operatorname{cl}(x)\mid x\in C\}\) constitue une partition de \(E\)
(Représentant, Partition - Système complet d’événements)